Hipérbola: definición y elementos

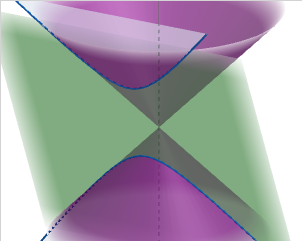
Una hipérbola es una sección de un cono.

Una hipérbola es también un lugar geométrico.

Definición: Dados dos puntos fijos F y F', llamados focos y una constante que llamaremos 2a, se llama hipérbola al lugar geométrico de los puntos del plano cuya diferencia de distancia (en valor absoluto) a los dos puntos fijos (F y F') es constante (2a).

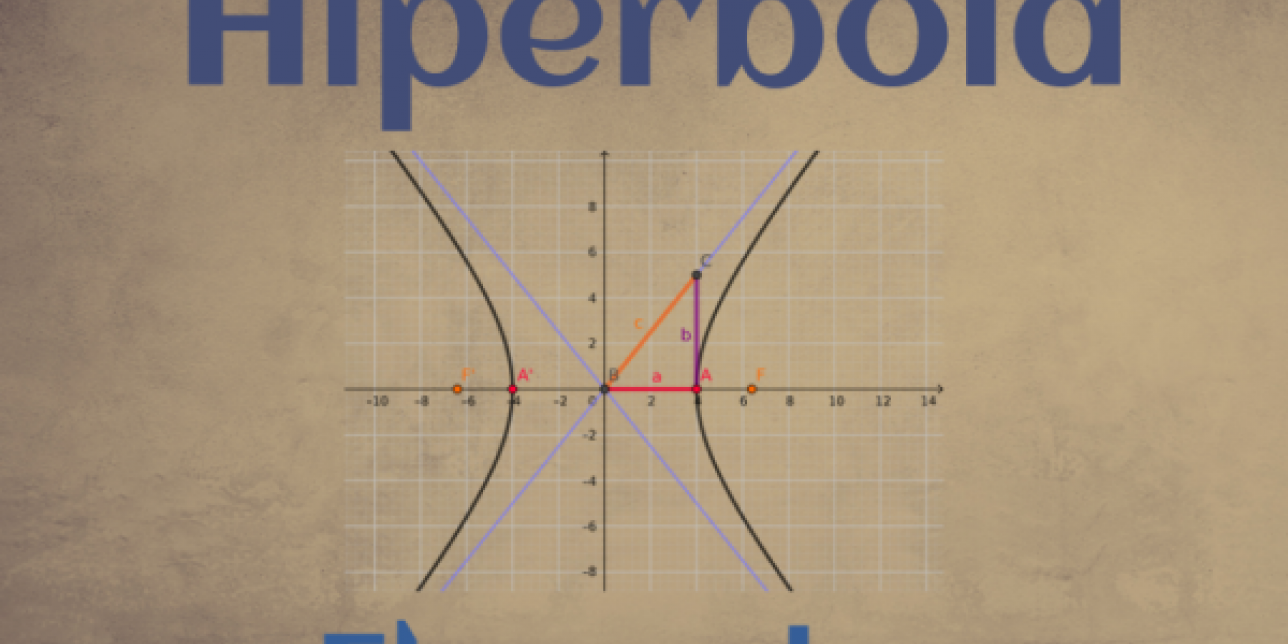
Veamos a través del siguiente applet los elementos de una hipérbola y los parámetros que la definen. 

Actividad

• Veamos primero que esta cónica es simétrica respecto a dos ejes haciendo clic en la casilla: Ejes de Simetría.
• La intersección de dichos ejes es el centro de la cónica. Haz clic en la casilla: Centro.
   
• Dichos ejes cortan a la cónica en dos puntos que llamaremos vértices de la misma: A y A'. Haz clic en la casilla: Vértices.
   
• Según la definición planteada anteriormente, para determinar hipérbola necesitamos dos puntos F y F' que llamaremos focos. Haz clic en la casilla: Focos.
  La distancia entre F y F' se llama 2c. Por simetría, la distancia de un foco al centro es igual que la distancia del otro foco al centro, así que la distancia entre un foco y el centro es c.
  
  Mueve los focos y el vértice A para ver cómo varía la forma de la hipérbola según la posición de ellos.
   
• El segmento que determinan los vértices A y A' se llama eje real de la hipérbola.
  Observa que como el punto A pertenece a la hipérbola va a cumplir la definición así que:
  |d(A,F)-d(A,F')|= 2a  pero por simetría, d(A,F)=d(A',F') por lo que resulta que d(A,A')= 2a.
  
  Entonces por simetría:
• La distancia entre el centro y el vértice A es a y la distancia entre el centro y el foco F es c.
  
  Piensa: ¿a puede ser mayor que c? Mueve los puntos A y F para observar si es posible.
  
  Construyamos un triángulo rectángulo con un cateto a y la hipotenusa c. Haz clic en la casilla: Relación entre los parámetros, para verlo.
  Al otro cateto lo llamaremos b y se denomina semieje imaginario.
  ¿a puede ser mayor que b? ¿a puede ser menor que b? ¿pueden ser iguales a y b?
  Mueve los puntos A y F para observar si existe una relación entre esos dos parámetros.
   
• Hemos visto tres parámetros entonces, a (2a es la constante de la hipérbola y a es la mitad del eje real), b (la mitad del eje imaginario) y c (la mitad de la distancia entre los focos).
• Ahora si aplicamos el teorema de Pitágoras al triángulo que se observa encontraremos que :  
  
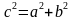
  Veamos ahora el último elemento de la hipérbola.
   
• Haz clic en la casilla Asíntotas para ver las dos asíntotas de la hipérbola y observa que las mismas pasan por el centro y tienen pendientes relacionadas con los parámetros b y a.
   
• Solo nos queda ver que los puntos de la hipérbola cumplen con la definición que dimos.
  Haz clic en la casilla: Constante y dale play a la animación que aparece en la esquina inferior izquierda. Observa qué pasa con el valor absoluto de las distancias de los puntos P de la hipérbola a los focos.
  
  
  Bibliografía:
  Guzmán, M., Cólera, J. y Salvador, A. (1998). Matemática. Bachillerato 3. Madrid. Grupo Anaya S.A.